Introducing the Fisheries Integrated Modeling System (FIMS) • FIMS

FIMS

The NOAA Fisheries Integrated Modeling System (FIMS) is a new modeling framework for fisheries modeling. The framework is designed to support next-generation fisheries stock assessment, ecosystem, and socioeconomic modeling. It is important to note that FIMS itself is not a model but rather a framework for creating models. The framework is made up of many modules that come together to create a model that best suits the needs of the end-user. The remainder of this vignette walks through what is absolutely necessary to run a FIMS catch-at-age model using the default settings.

Memory

Calling library(FIMS) loads the R package and Rcpp functions and modules into the R environment. The C++ code is compiled upon installation rather than loading so the call to library() should be pretty fast. Users should always run clear() prior to modeling to ensure that the C++ memory from any previous FIMS model run is cleared out.

library(FIMS)
library(ggplot2)
library(stockplotr)

# Use the {stockplotr} theme for all figures
# ggplot2::theme_set(stockplotr::theme_noaa())


# clear memory
clear()

Data

Data for a FIMS model must be stored in a single data frame with a long format, e.g., data("data1", package = "FIMS"). The design is similar to running a linear model where you pass a single data frame to lm(). The long format does lead to some information being duplicated. For example, the units are listed for every row rather than stored in a single location for each data type. But, the long format facilitates using tidy functions to manipulate the data. And, a single function, i.e., FIMSFrame(), is all that is needed to prepare the data to be used in a FIMS model.

`data1`

A sample data frame for a catch-at-age model with both ages and lengths is stored in the package as data1. This data set is based on data that was used in Li et al. for the Model Comparison Project (github site). The length data have since been added data-raw/data1.R based on an age-length conversion matrix. See R/data1.R or ?data1 for details about the package data.

`FIMSFrame()`

The easiest way to prepare the data for a FIMS model is to use FIMSFrame(). This function performs several validation checks and returns an object of the S4 class called FIMSFrame. There are helper functions for working with a FIMSFrame object, e.g., get_data(), get_n_years(), get_*(). Additionally, there are helper functions for pulling data out of the S4 class in the format needed for a module, i.e., a vector, but these m_*() functions are largely meant to be used internally within the package and are only exported to allow for their use by power users wishing to manually set up.

# Bring the package data into your environment
data("data1")
# Prepare the package data for being used in a FIMS model
data_4_model <- FIMSFrame(data1)

The S4 object that we named data_4_model contains many slots (i.e., named components of the object that can be accessed) but perhaps the most interesting one is the long data frame stored in the “data” slot. The tibble stored in this slot can be accessed using get_data().

# Use show() to see what is stored in the FIMSFrame S4 class
methods::show(data_4_model)

## tbl_df of class 'FIMSFrame'

## with the following 'types': age-to-length-conversion, age_comp, landings, length_comp, weight-at-age, index

## # A tibble: 6 × 8
##   type                     name     age length timing    value unit  uncertainty
##   <chr>                    <chr>  <int>  <dbl>  <int>    <dbl> <chr>       <dbl>
## 1 age-to-length-conversion fleet1     1      0      1 1.26e-16 prop…         200
## 2 age-to-length-conversion fleet1     1     50      1 8.39e-11 prop…         200
## 3 age-to-length-conversion fleet1     1    100      1 2.30e- 6 prop…         200
## 4 age-to-length-conversion fleet1     1    150      1 2.74e- 3 prop…         200
## 5 age-to-length-conversion fleet1     1    200      1 1.63e- 1 prop…         200
## 6 age-to-length-conversion fleet1     1    250      1 6.32e- 1 prop…         200
## additional slots include the following:fleets:
## [1] "fleet1"  "survey1"
## n_years:
## [1] 30
## ages:
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12
## n_ages:
## [1] 12
## lengths:
##  [1]    0   50  100  150  200  250  300  350  400  450  500  550  600  650  700
## [16]  750  800  850  900  950 1000 1050 1100
## n_lengths:
## [1] 23
## start_year:
## [1] 1
## end_year:
## [1] 30

# Or, look at the structure using str()
# Increase max.level to see more of the structure
str(data_4_model, max.level = 1)

## Formal class 'FIMSFrame' [package "FIMS"] with 9 slots

# Use dplyr to subset the data for just the landings
get_data(data_4_model) |>
  dplyr::filter(type == "landings")

## # A tibble: 30 × 8
##    type     name     age length timing value unit  uncertainty
##    <chr>    <chr>  <int>  <dbl>  <int> <dbl> <chr>       <dbl>
##  1 landings fleet1    NA     NA      1  162. mt        0.01000
##  2 landings fleet1    NA     NA      2  461. mt        0.01000
##  3 landings fleet1    NA     NA      3  747. mt        0.01000
##  4 landings fleet1    NA     NA      4  997. mt        0.01000
##  5 landings fleet1    NA     NA      5  768. mt        0.01000
##  6 landings fleet1    NA     NA      6 1344. mt        0.01000
##  7 landings fleet1    NA     NA      7 1319. mt        0.01000
##  8 landings fleet1    NA     NA      8 2598. mt        0.01000
##  9 landings fleet1    NA     NA      9 1426. mt        0.01000
## 10 landings fleet1    NA     NA     10 1644. mt        0.01000
## # ℹ 20 more rows

The data contains the following fleets:

A single fishery fleet with age- and length-composition, weight-at-age, and landings data
A single survey with age- and length-composition and index data

configurations

`create_default_configurations()`

The create_default_configurations() function is designed to generate a set of default configurations for the various components of a FIMS model. This includes configurations for fleets, growth, maturity, and recruitment modules. By leveraging the structure of the input data, the function can automatically set up initial configurations for each module. By passing the data and configurations to create_default_parameters() the function can tailor the defaults based on how many fleets there are and what data types exist. For example, if you have three fleets, then create_default_configurations() will set up three logistic selectivity modules.

# Create default configurations based on the data
default_configurations <- create_default_configurations(data = data_4_model) |>
  print()

##  [38;5;246m# A tibble: 7 × 4 [39m
##   model_family module_name fleet_name data            
##    [3m [38;5;246m<chr> [39m [23m         [3m [38;5;246m<chr> [39m [23m        [3m [38;5;246m<chr> [39m [23m       [3m [38;5;246m<list> [39m [23m          
##  [38;5;250m1 [39m catch_at_age Data        fleet1      [38;5;246m<tibble [3 × 4]> [39m
##  [38;5;250m2 [39m catch_at_age Selectivity fleet1      [38;5;246m<tibble [1 × 4]> [39m
##  [38;5;250m3 [39m catch_at_age Data        survey1     [38;5;246m<tibble [3 × 4]> [39m
##  [38;5;250m4 [39m catch_at_age Selectivity survey1     [38;5;246m<tibble [1 × 4]> [39m
##  [38;5;250m5 [39m catch_at_age Growth       [31mNA [39m          [38;5;246m<tibble [1 × 4]> [39m
##  [38;5;250m6 [39m catch_at_age Maturity     [31mNA [39m          [38;5;246m<tibble [1 × 4]> [39m
##  [38;5;250m7 [39m catch_at_age Recruitment  [31mNA [39m          [38;5;246m<tibble [1 × 4]> [39m

# The output is a nested tibble, with details in the `data` column.
default_configurations_unnested <- default_configurations |>
  tidyr::unnest(cols = data) |>
  print()

##  [38;5;246m# A tibble: 11 × 7 [39m
##    model_family module_name fleet_name module_type  distribution_link
##     [3m [38;5;246m<chr> [39m [23m         [3m [38;5;246m<chr> [39m [23m        [3m [38;5;246m<chr> [39m [23m       [3m [38;5;246m<chr> [39m [23m         [3m [38;5;246m<chr> [39m [23m            
##  [38;5;250m 1 [39m catch_at_age Data        fleet1     AgeComp      AgeComp          
##  [38;5;250m 2 [39m catch_at_age Data        fleet1     Landings     Landings         
##  [38;5;250m 3 [39m catch_at_age Data        fleet1     LengthComp   LengthComp       
##  [38;5;250m 4 [39m catch_at_age Selectivity fleet1     Logistic      [31mNA [39m               
##  [38;5;250m 5 [39m catch_at_age Data        survey1    AgeComp      AgeComp          
##  [38;5;250m 6 [39m catch_at_age Data        survey1    Index        Index            
##  [38;5;250m 7 [39m catch_at_age Data        survey1    LengthComp   LengthComp       
##  [38;5;250m 8 [39m catch_at_age Selectivity survey1    Logistic      [31mNA [39m               
##  [38;5;250m 9 [39m catch_at_age Growth       [31mNA [39m         EWAA          [31mNA [39m               
##  [38;5;250m10 [39m catch_at_age Maturity     [31mNA [39m         Logistic      [31mNA [39m               
##  [38;5;250m11 [39m catch_at_age Recruitment  [31mNA [39m         BevertonHolt log_devs         
##  [38;5;246m# ℹ 2 more variables: distribution_type <chr>, distribution <chr> [39m

Update configurations

The default_configurations are just a starting point. Functions (e.g., rows_*()) from dplyr can be used to modify the default configurations as needed. For example, logistic selectivity for survey1 can be changed to double logistic selectivity.

# Update the module_type for survey1's selectivity
updated_configurations <- default_configurations_unnested |>
  dplyr::rows_update(
    y = tibble::tibble(
      module_name = c("Selectivity"),
      fleet_name = c("survey1"),
      module_type = c("DoubleLogistic")
    ),
    by = c("module_name", "fleet_name")
  ) |>
  print()

##  [38;5;246m# A tibble: 11 × 7 [39m
##    model_family module_name fleet_name module_type    distribution_link
##     [3m [38;5;246m<chr> [39m [23m         [3m [38;5;246m<chr> [39m [23m        [3m [38;5;246m<chr> [39m [23m       [3m [38;5;246m<chr> [39m [23m           [3m [38;5;246m<chr> [39m [23m            
##  [38;5;250m 1 [39m catch_at_age Data        fleet1     AgeComp        AgeComp          
##  [38;5;250m 2 [39m catch_at_age Data        fleet1     Landings       Landings         
##  [38;5;250m 3 [39m catch_at_age Data        fleet1     LengthComp     LengthComp       
##  [38;5;250m 4 [39m catch_at_age Selectivity fleet1     Logistic        [31mNA [39m               
##  [38;5;250m 5 [39m catch_at_age Data        survey1    AgeComp        AgeComp          
##  [38;5;250m 6 [39m catch_at_age Data        survey1    Index          Index            
##  [38;5;250m 7 [39m catch_at_age Data        survey1    LengthComp     LengthComp       
##  [38;5;250m 8 [39m catch_at_age Selectivity survey1    DoubleLogistic  [31mNA [39m               
##  [38;5;250m 9 [39m catch_at_age Growth       [31mNA [39m         EWAA            [31mNA [39m               
##  [38;5;250m10 [39m catch_at_age Maturity     [31mNA [39m         Logistic        [31mNA [39m               
##  [38;5;250m11 [39m catch_at_age Recruitment  [31mNA [39m         BevertonHolt   log_devs         
##  [38;5;246m# ℹ 2 more variables: distribution_type <chr>, distribution <chr> [39m

# Nest updated_configurations
updated_configurations_nested <- updated_configurations |>
  tidyr::nest(.by = c(model_family, module_name, fleet_name))

Parameters

The parameters that are in the model will depend on which modules are used from the FIMS framework. This combination of modules rather than the use of a control file negates the need for complicated if{} else{} statements in the code.

`create_default_parameters()`

Modules that are available in FIMS are known as reference classes in the C++ code. Each reference class acts as an interface between R and the underlining C++ code that defines FIMS. Several reference classes exist and several more will be created in the future. The beauty of having modules rather than a control file really comes out when more reference classes are created because each reference class can be accessed through R by itself to build up a model rather than needing to modify a control file for future features.

By just passing the configurations and the data to create_default_parameters(), the default values for parameters that relate to fleet(s), recruitment, growth, and maturity modules can be created. For example,

“BevertonHolt” for the recruitment module
“Dnorm” distribution for recruitment deviations (log_devs)
“EWAA” for the Growth module, and
“Logistic” for Maturity module.

# Create default parameters based on default_configurations and data
default_parameters <- create_default_parameters(
  configurations = default_configurations,
  data = data_4_model
) |>
  print()

##  [38;5;246m# A tibble: 10 × 4 [39m
##    model_family module_name fleet_name data               
##     [3m [38;5;246m<chr> [39m [23m         [3m [38;5;246m<chr> [39m [23m        [3m [38;5;246m<chr> [39m [23m       [3m [38;5;246m<list> [39m [23m             
##  [38;5;250m 1 [39m catch_at_age Selectivity fleet1      [38;5;246m<tibble [2 × 10]> [39m  
##  [38;5;250m 2 [39m catch_at_age Fleet       fleet1      [38;5;246m<tibble [31 × 10]> [39m 
##  [38;5;250m 3 [39m catch_at_age Data        fleet1      [38;5;246m<tibble [32 × 10]> [39m 
##  [38;5;250m 4 [39m catch_at_age Selectivity survey1     [38;5;246m<tibble [2 × 10]> [39m  
##  [38;5;250m 5 [39m catch_at_age Fleet       survey1     [38;5;246m<tibble [31 × 10]> [39m 
##  [38;5;250m 6 [39m catch_at_age Data        survey1     [38;5;246m<tibble [32 × 10]> [39m 
##  [38;5;250m 7 [39m catch_at_age Recruitment  [31mNA [39m          [38;5;246m<tibble [150 × 10]> [39m
##  [38;5;250m 8 [39m catch_at_age Maturity     [31mNA [39m          [38;5;246m<tibble [2 × 10]> [39m  
##  [38;5;250m 9 [39m catch_at_age Population   [31mNA [39m          [38;5;246m<tibble [372 × 10]> [39m
##  [38;5;250m10 [39m catch_at_age Growth       [31mNA [39m          [38;5;246m<tibble [1 × 10]> [39m

# Unnest the default_parameters to see the detailed parameters
default_parameters_unnested <- tidyr::unnest(default_parameters, cols = data) |>
  print()

##  [38;5;246m# A tibble: 655 × 13 [39m
##    model_family module_name fleet_name module_type label distribution_link   age
##     [3m [38;5;246m<chr> [39m [23m         [3m [38;5;246m<chr> [39m [23m        [3m [38;5;246m<chr> [39m [23m       [3m [38;5;246m<chr> [39m [23m        [3m [38;5;246m<chr> [39m [23m  [3m [38;5;246m<chr> [39m [23m              [3m [38;5;246m<dbl> [39m [23m
##  [38;5;250m 1 [39m catch_at_age Selectivity fleet1     Logistic    infl…  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 2 [39m catch_at_age Selectivity fleet1     Logistic    slope  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 3 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_q  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 4 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_…  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 5 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_…  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 6 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_…  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 7 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_…  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 8 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_…  [31mNA [39m                    [31mNA [39m
##  [38;5;250m 9 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_…  [31mNA [39m                    [31mNA [39m
##  [38;5;250m10 [39m catch_at_age Fleet       fleet1      [31mNA [39m          log_…  [31mNA [39m                    [31mNA [39m
##  [38;5;246m# ℹ 645 more rows [39m
##  [38;5;246m# ℹ 6 more variables: length <dbl>, time <int>, value <dbl>, [39m
##  [38;5;246m#   estimation_type <chr>, distribution_type <chr>, distribution <chr> [39m

Update parameters

Functions (e.g., rows_*()) from dplyr can be used to update the default parameters as needed.

In the code below, rows_update() is used to adjust the fishing mortality, selectivity, maturity, and population parameters from their default values.

parameters_4_model <- default_parameters |>
  tidyr::unnest(cols = data) |>
  # Update log_Fmort initial values for Fleet1
  dplyr::rows_update(
    tibble::tibble(
      fleet_name = "fleet1",
      label = "log_Fmort",
      time = 1:30,
      value = log(c(
        0.009459165, 0.027288858, 0.045063639,
        0.061017825, 0.048600752, 0.087420554,
        0.088447204, 0.186607929, 0.109008958,
        0.132704335, 0.150615473, 0.161242955,
        0.116640187, 0.169346119, 0.180191913,
        0.161240483, 0.314573212, 0.257247574,
        0.254887252, 0.251462108, 0.349101406,
        0.254107720, 0.418478117, 0.345721184,
        0.343685540, 0.314171227, 0.308026829,
        0.431745298, 0.328030899, 0.499675368
      ))
    ),
    by = c("fleet_name", "label", "time")
  ) |>
  # Update selectivity parameters and log_q for survey1
  dplyr::rows_update(
    tibble::tibble(
      fleet_name = "survey1",
      label = c("inflection_point", "slope", "log_q"),
      value = c(1.5, 2, log(3.315143e-07))
    ),
    by = c("fleet_name", "label")
  ) |>
  # Update log_devs in the Recruitment module (time steps 2-30)
  dplyr::rows_update(
    tibble::tibble(
      label = "log_devs",
      time = 2:30,
      value = c(
        0.43787763, -0.13299042, -0.43251973, 0.64861200, 0.50640852,
        -0.06958319, 0.30246260, -0.08257384, 0.20740372, 0.15289604,
        -0.21709207, -0.13320626, 0.11225374, -0.10650836, 0.26877132,
        0.24094126, -0.54480751, -0.23680557, -0.58483386, 0.30122785,
        0.21930545, -0.22281699, -0.51358369, 0.15740234, -0.53988240,
        -0.19556523, 0.20094360, 0.37248740, -0.07163145
      )
    ),
    by = c("label", "time")
  ) |>
  # Update log_sd for log_devs in the Recruitment module
  dplyr::rows_update(
    tibble::tibble(
      module_name = "Recruitment",
      label = "log_sd",
      value = 0.4
    ),
    by = c("module_name", "label")
  ) |>
  # Update inflection point and slope parameters in the Maturity module
  dplyr::rows_update(
    tibble::tibble(
      module_name = "Maturity",
      label = c("inflection_point", "slope"),
      value = c(2.25, 3)
    ),
    by = c("module_name", "label")
  ) |>
  # Update log_init_naa values in the Population module
  dplyr::rows_update(
    tibble::tibble(
      label = "log_init_naa",
      age = 1:12,
      value = c(
        13.80944, 13.60690, 13.40217, 13.19525, 12.98692, 12.77791,
        12.56862, 12.35922, 12.14979, 11.94034, 11.73088, 13.18755
      )
    ),
    by = c("label", "age")
  )

Fit

With data and parameters in place, we can now initialize modules using initialize_fims() and fit the model using fit_fims().

`initialize_fims()`

The tibble returned by create_default_parameters() is just a data frame containing specifications. Nothing has been created in memory as of yet. To actually initialize the modules, initialize_fims() needs to be called. This function takes all of the specifications and matches them with the appropriate data to initialize a module and create the pointers to the memory.

`fit_fims()`

The list returned from initialize_fims() can be passed to the parameter of fit_fims() called input to run a FIMS model. If optimize = FALSE, the model will not actually be optimized but instead just checked to ensure it is a viable model. When optimize = TRUE, the model will be fit using stats::nlminb() and an object of the class FIMSFit will be returned.

Example

# Run the model without optimization to help ensure a viable model
test_fit <- parameters_4_model |>
  initialize_fims(data = data_4_model) |>
  fit_fims(optimize = FALSE)
clear()
# Run the  model with optimization
fit <- parameters_4_model |>
  initialize_fims(data = data_4_model) |>
  fit_fims(optimize = TRUE)

## ✔ Starting optimization ...
## ℹ Restarting optimizer 3 times to improve gradient.
## ℹ Maximum gradient went from 0.016 to 0.00333 after 3 steps.
## ✔ Finished optimization
## ✔ Finished sdreport
## ℹ FIMS model version: 0.7
## ℹ Total run time was 1.23037 minutes
## ℹ Number of parameters: fixed_effects=77, random_effects=0, and total=77
## ℹ Maximum gradient= 0.00333
## ℹ Negative log likelihood (NLL):
## • Marginal NLL= 3166.02383
## • Total NLL= 3166.02383
## ℹ Terminal SB=

clear()

# Get information about the model and print a few characters to the screen
recruitment_log <- get_log_module("information")
substr(recruitment_log, 1, 100)

## [1] "[\n]"

The results can be plotted with either base R, {ggplot2}, or {stockplotr}. Where, we recommend using {stockplotr} where possible.

# Temporary manipulation to the returned estimates to get them
# to work with stockplotr
output <- get_estimates(fit) |>
  dplyr::mutate(
    uncertainty_label = "se",
    year = year_i,
    estimate = estimated
  )

# Plot spawning biomass
stockplotr::plot_spawning_biomass(
  dplyr::filter(output, label == "spawning_biomass")
) +
  stockplotr::theme_noaa()

## Warning: Unknown or uninitialised column: `era`.

## Warning in max(dat$year[dat$era == era_name], na.rm = TRUE): no non-missing
## arguments to max; returning -Inf

## Scale for colour is already present.
## Adding another scale for colour, which will replace the existing scale.
## Scale for fill is already present.
## Adding another scale for fill, which will replace the existing scale.

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_hline()`).

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_text()`).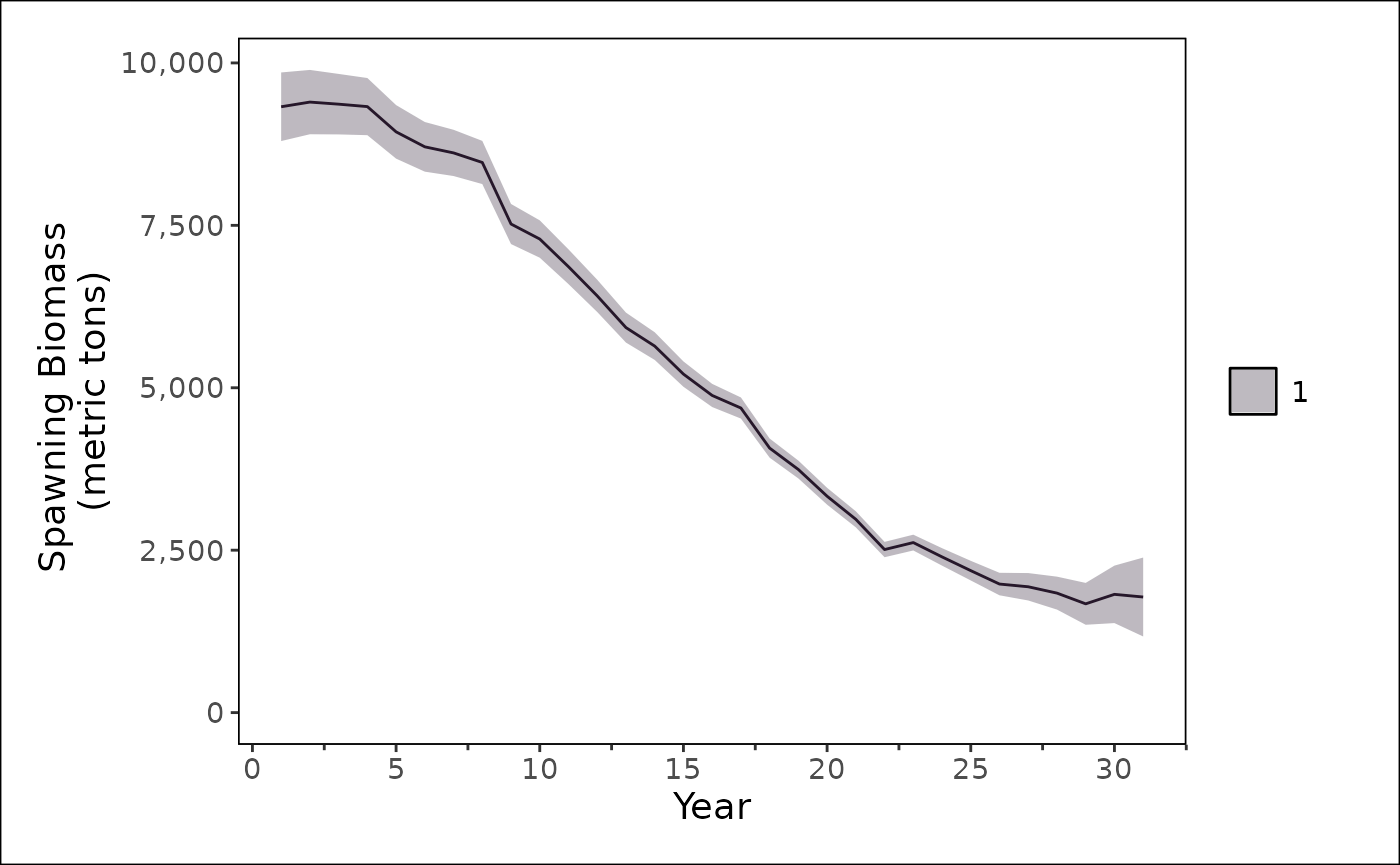

# Plot of log fishing mortality
stockplotr::plot_timeseries(
  stockplotr::filter_data(
    output |> dplyr::filter(module_id == 1),
    label_name = "log_Fmort$",
    geom = "line"
  ),
  x = "year",
  y = "estimate",
  ylab = "natural log of Fishing Mortality"
) +
  stockplotr::theme_noaa()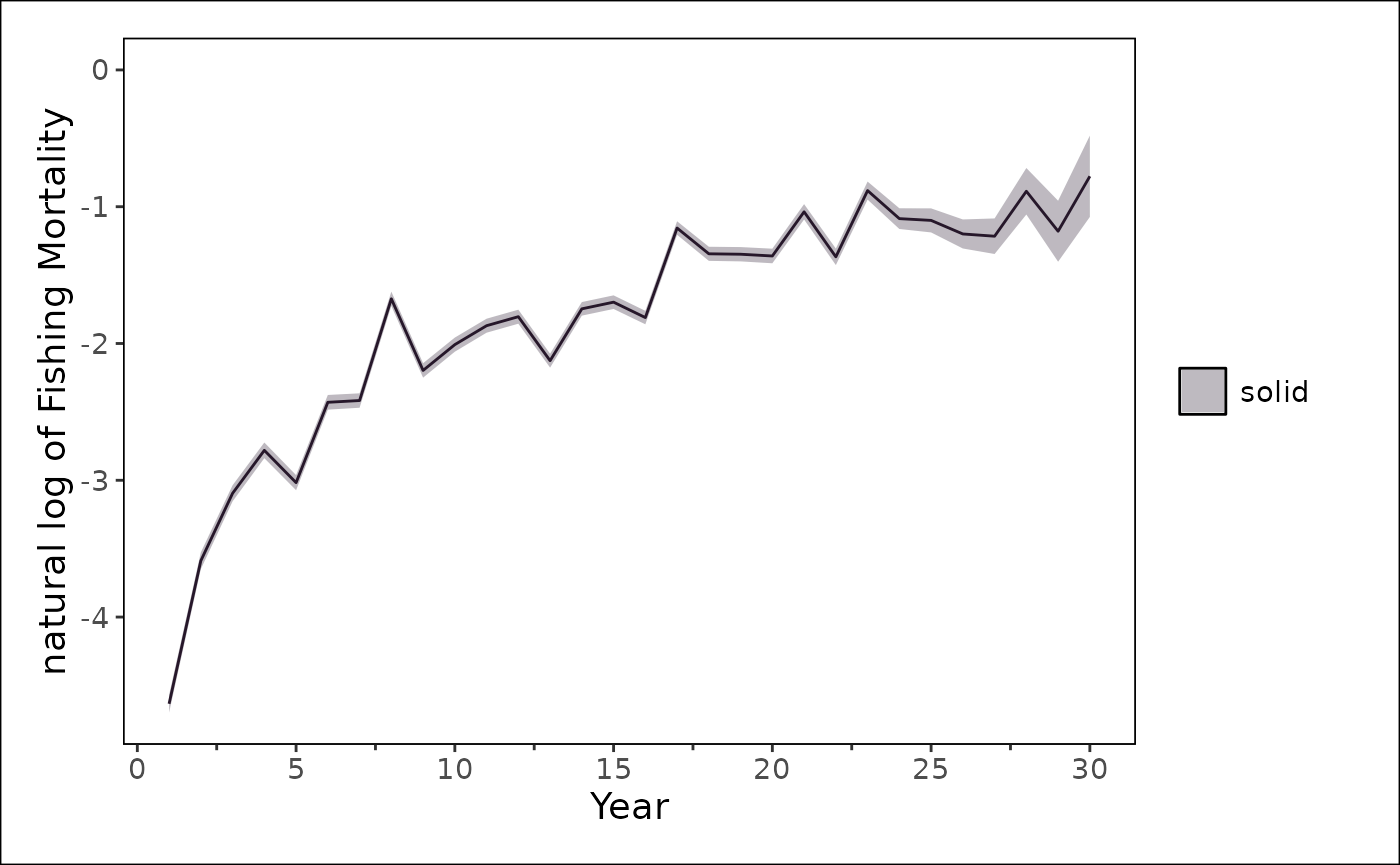

# Plot the index of abundance against the observed values
stockplotr::plot_timeseries(
  stockplotr::filter_data(
    output |> dplyr::filter(module_id == 2),
    label_name = "^index_expected$",
    geom = "line"
  ),
  x = "year",
  y = "estimate",
  ylab = "Relative Index of Abundance"
) +
  ggplot2::geom_point(
    data = data.frame(
      observed = m_index(data_4_model, "survey1"),
      expected = get_report(fit)[["index_expected"]][[2]],
      year = get_start_year(data_4_model):get_end_year(data_4_model)
    ),
    ggplot2::aes(x = year, y = observed)
  ) +
  stockplotr::theme_noaa()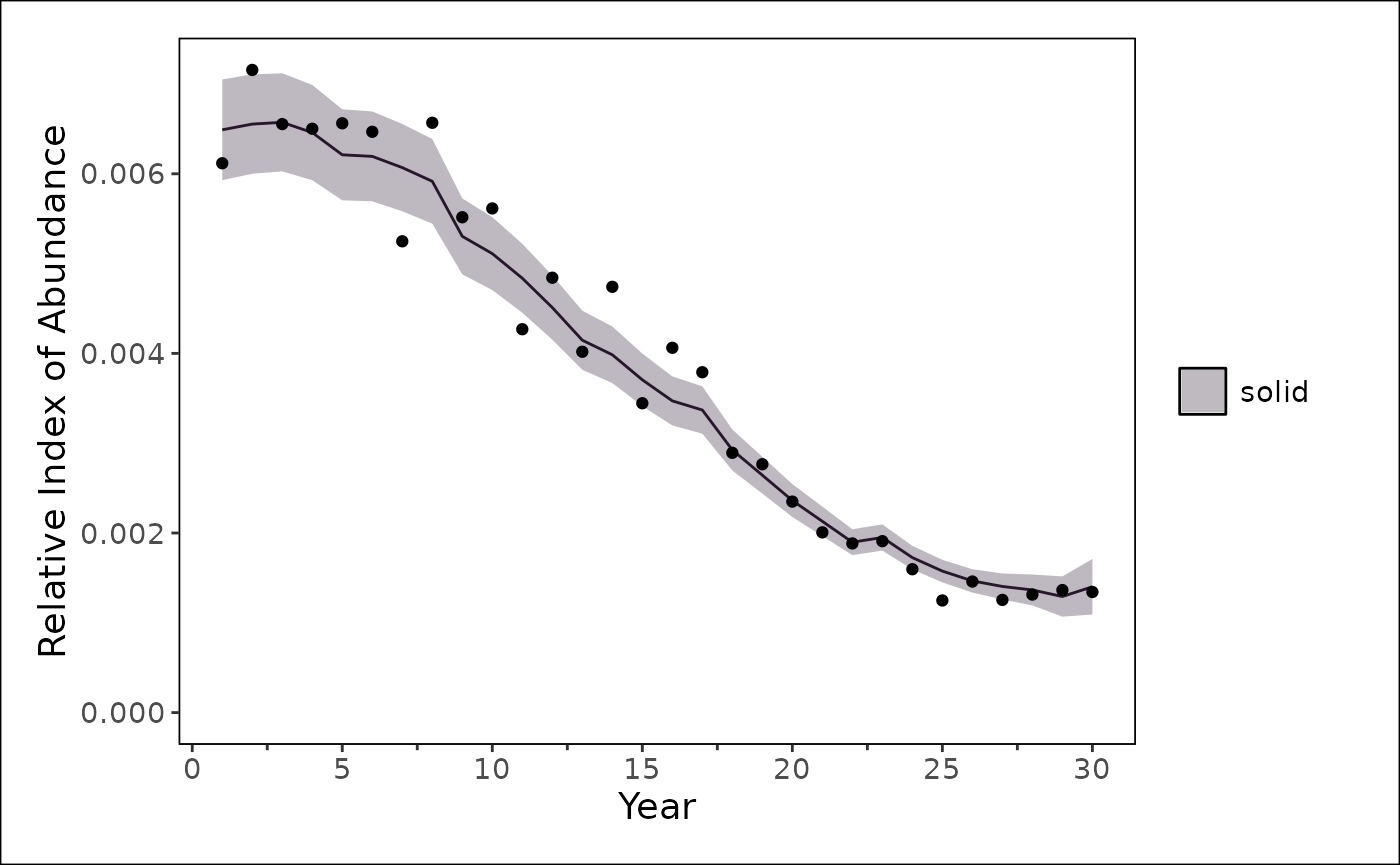

# Plot the landings estimates
stockplotr::plot_timeseries(
  stockplotr::filter_data(
    output |> dplyr::filter(module_id == 1),
    label_name = "^landings_expected$",
    geom = "line"
  ),
  x = "year",
  y = "estimate",
  ylab = "Expected Landings (mt)"
) +
  stockplotr::theme_noaa()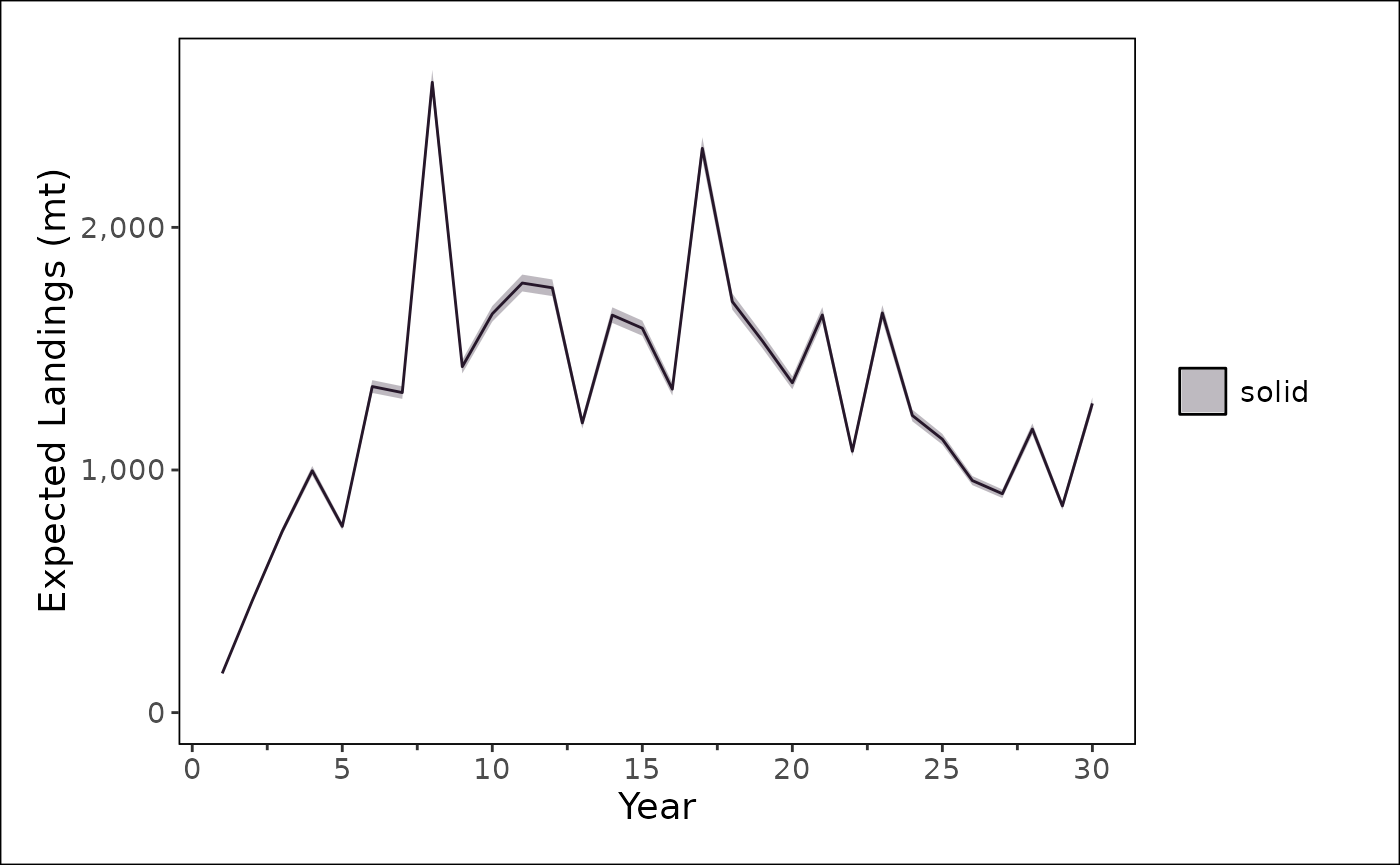

Sensitivities

Multiple fits, i.e., sensitivity runs, can be set up by modifying the parameter list using update_parameters() or changing the data that is used to fit the model.

Initial values

For example, one could change the initial value used for the slope of the logistic curve for the survey to see if the terminal estimate changes due to changes to the initial value.

parameters_high_slope <- parameters_4_model |>
  # Update the slope value of the logistic selectivity for the survey
  dplyr::mutate(
    value = dplyr::if_else(
      module_name == "Selectivity" &
        fleet_name == "survey1" &
        label == "slope",
      2.5,
      value
    )
  )

parameters_low_slope <- parameters_4_model |>
  dplyr::mutate(
    value = dplyr::if_else(
      module_name == "Selectivity" &
        fleet_name == "survey1" &
        label == "slope",
      1,
      value
    )
  )

high_slope_fit <- parameters_high_slope |>
  initialize_fims(data = data_4_model) |>
  fit_fims(optimize = TRUE)

## ✔ Starting optimization ...
## ℹ Restarting optimizer 3 times to improve gradient.
## ℹ Maximum gradient went from 0.01439 to 0.00073 after 3 steps.
## ✔ Finished optimization
## ✔ Finished sdreport
## ℹ FIMS model version: 0.7
## ℹ Total run time was 1.21054 minutes
## ℹ Number of parameters: fixed_effects=77, random_effects=0, and total=77
## ℹ Maximum gradient= 0.00073
## ℹ Negative log likelihood (NLL):
## • Marginal NLL= 3166.02383
## • Total NLL= 3166.02383
## ℹ Terminal SB=

clear()

low_slope_fit <- parameters_low_slope |>
  initialize_fims(data = data_4_model) |>
  fit_fims(optimize = TRUE)

## ✔ Starting optimization ...
## ℹ Restarting optimizer 3 times to improve gradient.
## ℹ Maximum gradient went from 0.03193 to 0.00022 after 3 steps.
## ✔ Finished optimization
## ✔ Finished sdreport
## ℹ FIMS model version: 0.7
## ℹ Total run time was 1.20888 minutes
## ℹ Number of parameters: fixed_effects=77, random_effects=0, and total=77
## ℹ Maximum gradient= 0.00022
## ℹ Negative log likelihood (NLL):
## • Marginal NLL= 3166.02383
## • Total NLL= 3166.02383
## ℹ Terminal SB=

clear()

Age only

The same model can be fit to just the age data, removing the length-composition configurations.

# Create default parameters, update with modified values, initialize FIMS,
# and fit the model
age_only_fit <- parameters_4_model |>
  # remove rows that have module_type == LengthComp
  dplyr::rows_delete(
    y = tibble::tibble(module_type = "LengthComp")
  ) |>
  initialize_fims(data = data_4_model) |>
  fit_fims(optimize = TRUE)

## Matching, by = "module_type"
## ✔ Starting optimization ...
## ℹ Restarting optimizer 3 times to improve gradient.
## ℹ Maximum gradient went from 0.01395 to 0.00219 after 3 steps.
## ✔ Finished optimization
## ✔ Finished sdreport
## ℹ FIMS model version: 0.7 ℹ Total run time was 9.02259 seconds ℹ Number of
## parameters: fixed_effects=77, random_effects=0, and total=77 ℹ Maximum
## gradient= 0.00219 ℹ Negative log likelihood (NLL): • Marginal NLL= 1565.4676 •
## Total NLL= 1565.4676 ℹ Terminal SB=

clear()

Length

The same model can be fit to just the length data, removing the age-composition configurations.

# Create default parameters, update with modified values, initialize FIMS,
# and fit the model
length_only_fit <- parameters_4_model |>
  # remove rows that have module_type == AgeComp
  dplyr::rows_delete(
    y = tibble::tibble(module_type = "AgeComp")
  ) |>
  initialize_fims(data = data_4_model) |>
  fit_fims(optimize = TRUE)

## Matching, by = "module_type"
## ✔ Starting optimization ...
## ℹ Restarting optimizer 3 times to improve gradient.
## ℹ Maximum gradient went from 0.02853 to 0.00013 after 3 steps.
## ✔ Finished optimization
## ✔ Finished sdreport
## ℹ FIMS model version: 0.7 ℹ Total run time was 56.61147 seconds ℹ Number of
## parameters: fixed_effects=77, random_effects=0, and total=77 ℹ Maximum
## gradient= 0.00013 ℹ Negative log likelihood (NLL): • Marginal NLL= 1520.03751 •
## Total NLL= 1520.03751 ℹ Terminal SB=

clear()

# Plot spawning biomass for each sensitivity model
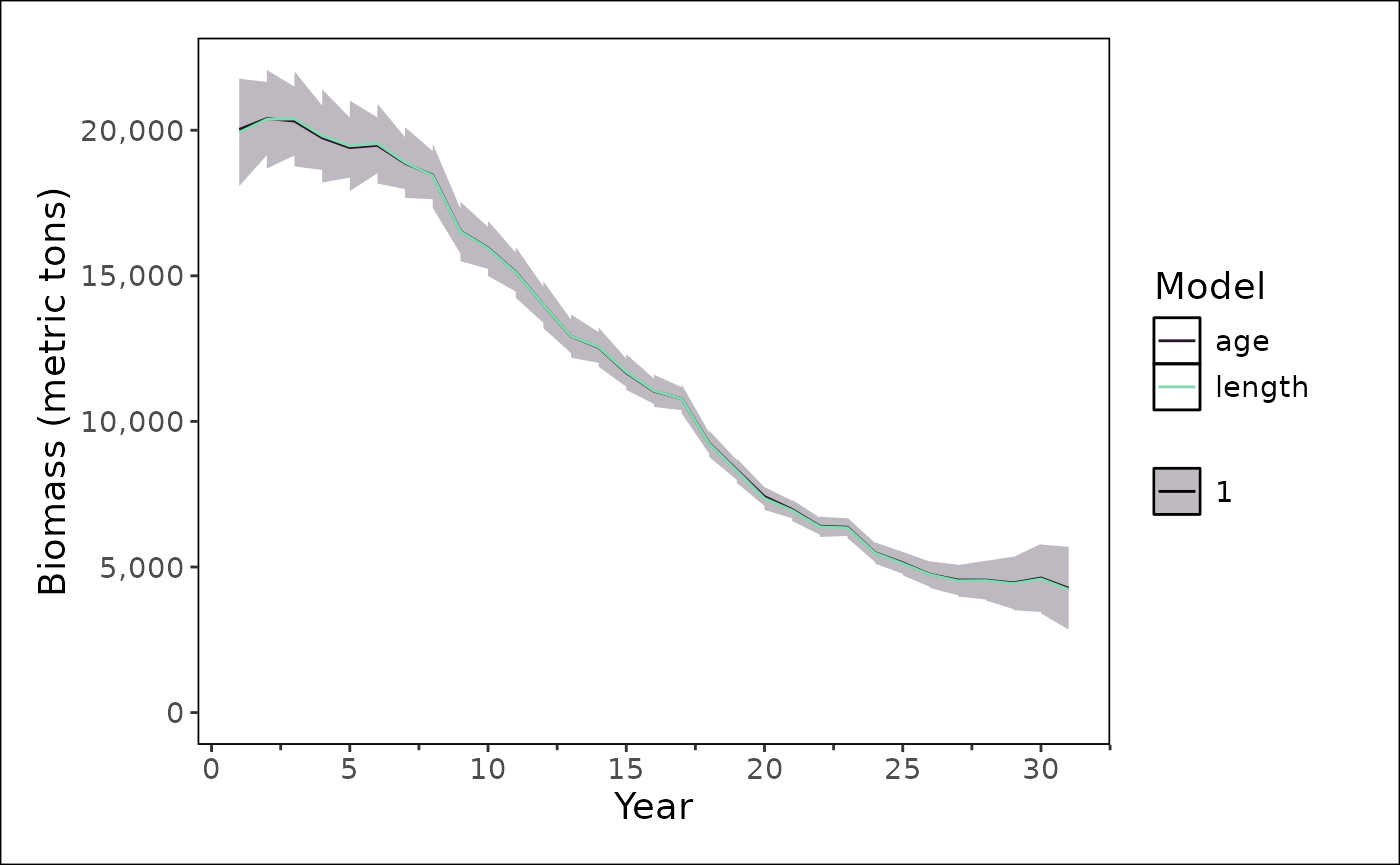
stockplotr::plot_biomass(
  list(
    "age" = get_estimates(age_only_fit) |>
      dplyr::mutate(
        uncertainty_label = "se",
        year = year_i,
        estimate = estimated
      ),
    "length" = get_estimates(length_only_fit) |>
      dplyr::mutate(
        uncertainty_label = "se",
        year = year_i,
        estimate = estimated
      )
  )
)

## Warning: Unknown or uninitialised column: `era`.

## Warning in max(dat$year[dat$era == era_name], na.rm = TRUE): no non-missing
## arguments to max; returning -Inf

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_hline()`).

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_text()`).