# Set up a FIMS model without wrapper functions
# the original model (with data)
mle <- opt$par
# TODO: Kelli is getting the error
# Hessian not yet implemented for models with random effects
hess <- obj$he(mle)
## make FIMS model without any data, only hyperdistribution on recdevs
FIMS::clear()
# Set up the model structure, copied from above
data_4_model <- prepare_pollock_data(
pkfitfinal = pkfitfinal,
pkfit0 = pkfit0,
parfinal = parfinal,
fimsdat = fimsdat,
pkinput = pkinput,
# A hack to trick the script to thinking there's no data
# (it should all be -999)
years = 500:1000,
n_years = n_years,
ages = ages,
n_ages = n_ages
)
fishery_catch <- FIMS::m_landings(data_4_model, "fleet1")
fishery_agecomp <- FIMS::m_agecomp(data_4_model, "fleet1")
survey_index2 <- FIMS::m_index(data_4_model, "survey2")
survey_agecomp2 <- FIMS::m_agecomp(data_4_model, "survey2")
survey_index3 <- FIMS::m_index(data_4_model, "survey3")
survey_agecomp3 <- FIMS::m_agecomp(data_4_model, "survey3")
survey_index6 <- FIMS::m_index(data_4_model, "survey6")
survey_agecomp6 <- FIMS::m_agecomp(data_4_model, "survey6")
# need to think about how to deal with multiple fleets - only using 1 fleet for now
# TODO: FIMS now supports multiple fishing fleets.
# We can test this feature using the case study to evaluate its functionality.
fish_index <- methods::new(Index, n_years)
fish_age_comp <- methods::new(AgeComp, n_years, n_ages)
purrr::walk(
seq_along(fishery_catch),
\(x) fish_index$index_data$set(x - 1, fishery_catch[x])
)
purrr::walk(
seq_along(fishery_agecomp),
\(x) fish_age_comp$age_comp_data$set(
x - 1,
(fishery_agecomp *
dplyr::filter(
.data = get_data(data_4_model),
type == "age_comp",
name %in% "fleet1"
) |>
dplyr::pull(value)
)[x]
)
)
### set up fishery
## fleet selectivity: converted from time-varying ascending
## slope/intercept to constant double-logistic
## methods::show(DoubleLogisticSelectivity)
fish_selex <- methods::new(DoubleLogisticSelectivity)
fish_selex$inflection_point_asc[1]$value <- parfinal$inf1_fsh_mean
fish_selex$inflection_point_asc[1]$estimation_type$set(estimate_fish_selex)
fish_selex$inflection_point_desc[1]$value <- parfinal$inf2_fsh_mean
fish_selex$inflection_point_desc[1]$estimation_type$set(estimate_fish_selex)
fish_selex$slope_asc[1]$value <- exp(parfinal$log_slp1_fsh_mean)
fish_selex$slope_asc[1]$estimation_type$set(estimate_fish_selex)
fish_selex$slope_desc[1]$value <- exp(parfinal$log_slp2_fsh_mean)
fish_selex$slope_desc[1]$estimation_type$set(estimate_fish_selex)
## create fleet object
fish_fleet <- methods::new(Fleet)
fish_fleet$nages$set(n_ages)
fish_fleet$nyears$set(n_years)
fish_fleet$log_Fmort$resize(n_years)
for (y in seq(n_years)) {
# Log-transform OM fishing mortality
fish_fleet$log_Fmort[y]$value <- log(pkfitfinal$rep$F[y])
}
fish_fleet$log_Fmort$set_all_estimable(TRUE)
fish_fleet$log_q[1]$value <- 0 # why is this length two in Chris' case study?
fish_fleet$log_q[1]$estimation_type$set("constant")
# Set Index, AgeComp, and Selectivity using the IDs from the modules defined above
fish_fleet$SetObservedIndexDataID(fish_index$get_id())
fish_fleet$SetObservedAgeCompDataID(fish_age_comp$get_id())
fish_fleet$SetSelectivityID(fish_selex$get_id())
# Set up fishery index data using the lognormal
fish_fleet_index_distribution <- methods::new(DlnormDistribution)
# lognormal observation error transformed on the log scale
fish_fleet_index_distribution$log_sd$resize(n_years)
for (y in seq(n_years)) {
# Compute lognormal SD from OM coefficient of variation (CV)
fish_fleet_index_distribution$log_sd[y]$value <- log(landings$uncertainty[y])
}
fish_fleet_index_distribution$log_sd$set_all_estimable(FALSE)
# Set Data using the IDs from the modules defined above
fish_fleet_index_distribution$set_observed_data(fish_fleet$GetObservedIndexDataID())
fish_fleet_index_distribution$set_distribution_links("data", fish_fleet$log_index_expected$get_id())
# Set up fishery age composition data using the multinomial
fish_fleet_agecomp_distribution <- methods::new(DmultinomDistribution)
fish_fleet_agecomp_distribution$set_observed_data(fish_fleet$GetObservedAgeCompDataID())
fish_fleet_agecomp_distribution$set_distribution_links("data", fish_fleet$agecomp_proportion$get_id())
## Setup survey 2
survey2_fleet_index <- methods::new(Index, n_years)
survey2_age_comp <- methods::new(AgeComp, n_years, n_ages)
purrr::walk(
seq_along(survey_index2),
\(x) survey2_fleet_index$index_data$set(x - 1, survey_index2[x])
)
purrr::walk(
seq_along(survey_agecomp2),
\(x) survey2_age_comp$age_comp_data$set(
x - 1,
(survey_agecomp2 *
dplyr::filter(
.data = get_data(data_4_model),
type == "age_comp",
name %in% "survey2"
) |>
dplyr::pull(value)
)[x]
)
)
## survey selectivity: ascending logistic
## methods::show(DoubleLogisticSelectivity)
survey2_selex <- methods::new(DoubleLogisticSelectivity)
survey2_selex$inflection_point_asc[1]$value <- parfinal$inf1_srv2
survey2_selex$inflection_point_asc[1]$estimation_type$set(estimate_survey_selex)
survey2_selex$slope_asc[1]$value <- exp(parfinal$log_slp1_srv2)
survey2_selex$slope_asc[1]$estimation_type$set(estimate_survey_selex)
## not estimated to make it ascending only, fix at input values
survey2_selex$inflection_point_desc[1]$value <- parfinal$inf2_srv2
survey2_selex$inflection_point_desc[1]$estimation_type$set("constant")
survey2_selex$slope_desc[1]$value <- exp(parfinal$log_slp2_srv2)
survey2_selex$slope_desc[1]$estimation_type$set("constant")
survey2_fleet <- methods::new(Fleet)
survey2_fleet$nages$set(n_ages)
survey2_fleet$nyears$set(n_years)
survey2_fleet$log_q[1]$value <- parfinal$log_q2_mean
survey2_fleet$log_q[1]$estimation_type$set("fixed_effects")
survey2_fleet$SetSelectivityID(survey2_selex$get_id())
survey2_fleet$SetObservedIndexDataID(survey2_fleet_index$get_id())
survey2_fleet$SetObservedAgeCompDataID(survey2_age_comp$get_id())
survey2_fleet_index_distribution <- methods::new(DlnormDistribution)
# lognormal observation error transformed on the log scale
survey2_fleet_index_distribution$log_sd$resize(n_years)
for (y in seq(n_years)) {
# Compute lognormal SD from OM coefficient of variation (CV)
survey2_fleet_index_distribution$log_sd[y]$value <- log(index2$uncertainty)[y]
}
survey2_fleet_index_distribution$log_sd$set_all_estimable(FALSE)
# Set Data using the IDs from the modules defined above
survey2_fleet_index_distribution$set_observed_data(survey2_fleet$GetObservedIndexDataID())
survey2_fleet_index_distribution$set_distribution_links("data", survey2_fleet$log_index_expected$get_id())
# Set up fishery age composition data using the multinomial
survey2_fleet_agecomp_distribution <- methods::new(DmultinomDistribution)
survey2_fleet_agecomp_distribution$set_observed_data(survey2_fleet$GetObservedAgeCompDataID())
survey2_fleet_agecomp_distribution$set_distribution_links("data", survey2_fleet$agecomp_proportion$get_id())
## Setup survey 3
survey3_fleet_index <- methods::new(Index, n_years)
survey3_age_comp <- methods::new(AgeComp, n_years, n_ages)
purrr::walk(
seq_along(survey_index3),
\(x) survey3_fleet_index$index_data$set(x - 1, survey_index3[x])
)
purrr::walk(
seq_along(survey_agecomp3),
\(x) survey3_age_comp$age_comp_data$set(
x - 1,
(survey_agecomp3 *
dplyr::filter(
.data = get_data(data_4_model),
type == "age_comp",
name %in% "survey3"
) |>
dplyr::pull(value)
)[x]
)
)
## survey selectivity: ascending logistic
## methods::show(LogisticSelectivity)
survey3_selex <- methods::new(LogisticSelectivity)
survey3_selex$inflection_point[1]$value <- parfinal$inf1_srv3
survey3_selex$inflection_point[1]$estimation_type$set(estimate_survey_selex)
survey3_selex$slope[1]$value <- exp(parfinal$log_slp1_srv3)
survey3_selex$slope[1]$estimation_type$set(estimate_survey_selex)
survey3_fleet <- methods::new(Fleet)
survey3_fleet$nages$set(n_ages)
survey3_fleet$nyears$set(n_years)
survey3_fleet$log_q[1]$value <- parfinal$log_q3_mean
survey3_fleet$log_q[1]$estimation_type$set("fixed_effects")
survey3_fleet$SetSelectivityID(survey3_selex$get_id())
survey3_fleet$SetObservedIndexDataID(survey3_fleet_index$get_id())
survey3_fleet$SetObservedAgeCompDataID(survey3_age_comp$get_id())
# sd = sqrt(log(cv^2 + 1)), sd is log transformed
survey3_fleet_index_distribution <- methods::new(DlnormDistribution)
# lognormal observation error transformed on the log scale
survey3_fleet_index_distribution$log_sd$resize(n_years)
for (y in seq(n_years)) {
# Compute lognormal SD from OM coefficient of variation (CV)
survey3_fleet_index_distribution$log_sd[y]$value <- log(index3$uncertainty)[y]
}
survey3_fleet_index_distribution$log_sd$set_all_estimable(FALSE)
# Set Data using the IDs from the modules defined above
survey3_fleet_index_distribution$set_observed_data(survey3_fleet$GetObservedIndexDataID())
survey3_fleet_index_distribution$set_distribution_links("data", survey3_fleet$log_index_expected$get_id())
# Set up fishery age composition data using the multinomial
survey3_fleet_agecomp_distribution <- methods::new(DmultinomDistribution)
survey3_fleet_agecomp_distribution$set_observed_data(survey3_fleet$GetObservedAgeCompDataID())
survey3_fleet_agecomp_distribution$set_distribution_links("data", survey3_fleet$agecomp_proportion$get_id())
## Setup survey 6
survey6_fleet_index <- methods::new(Index, n_years)
survey6_age_comp <- methods::new(AgeComp, n_years, n_ages)
purrr::walk(
seq_along(survey_index6),
\(x) survey6_fleet_index$index_data$set(x - 1, survey_index6[x])
)
purrr::walk(
seq_along(survey_agecomp6),
\(x) survey6_age_comp$age_comp_data$set(
x - 1,
(survey_agecomp6 *
dplyr::filter(
.data = get_data(data_4_model),
type == "age_comp",
name %in% "survey6"
) |>
dplyr::pull(value)
)[x]
)
)
## survey selectivity: ascending logistic
## methods::show(DoubleLogisticSelectivity)
survey6_selex <- methods::new(DoubleLogisticSelectivity)
survey6_selex$inflection_point_asc[1]$value <- parfinal$inf1_srv6
survey6_selex$inflection_point_asc[1]$estimation_type$set("constant")
survey6_selex$slope_asc[1]$value <- exp(parfinal$log_slp1_srv6)
survey6_selex$slope_asc[1]$estimation_type$set("constant")
## not estimated to make it ascending only, fix at input values
survey6_selex$inflection_point_desc[1]$value <- parfinal$inf2_srv6
survey6_selex$inflection_point_desc[1]$estimation_type$set(estimate_survey_selex)
survey6_selex$slope_desc[1]$value <- exp(parfinal$log_slp2_srv6)
survey6_selex$slope_desc[1]$estimation_type$set(estimate_survey_selex)
survey6_fleet <- methods::new(Fleet)
survey6_fleet$nages$set(n_ages)
survey6_fleet$nyears$set(n_years)
survey6_fleet$log_q[1]$value <- parfinal$log_q6
survey6_fleet$log_q[1]$estimation_type$set("fixed_effects")
survey6_fleet$SetSelectivityID(survey6_selex$get_id())
survey6_fleet$SetObservedIndexDataID(survey6_fleet_index$get_id())
survey6_fleet$SetObservedAgeCompDataID(survey6_age_comp$get_id())
survey6_fleet_index_distribution <- methods::new(DlnormDistribution)
# lognormal observation error transformed on the log scale
survey6_fleet_index_distribution$log_sd$resize(n_years)
for (y in seq(n_years)) {
# Compute lognormal SD from OM coefficient of variation (CV)
survey6_fleet_index_distribution$log_sd[y]$value <- log(index6$uncertainty)[y]
}
survey6_fleet_index_distribution$log_sd$set_all_estimable(FALSE)
# Set Data using the IDs from the modules defined above
survey6_fleet_index_distribution$set_observed_data(survey6_fleet$GetObservedIndexDataID())
survey6_fleet_index_distribution$set_distribution_links("data", survey6_fleet$log_index_expected$get_id())
# Set up fishery age composition data using the multinomial
survey6_fleet_agecomp_distribution <- methods::new(DmultinomDistribution)
survey6_fleet_agecomp_distribution$set_observed_data(survey6_fleet$GetObservedAgeCompDataID())
survey6_fleet_agecomp_distribution$set_distribution_links("data", survey6_fleet$agecomp_proportion$get_id())
# Population module
# recruitment
recruitment <- methods::new(BevertonHoltRecruitment)
recruitment_process <- methods::new(LogDevsRecruitmentProcess)
recruitment$SetRecruitmentProcessID(recruitment_process$get_id())
## methods::show(BevertonHoltRecruitment)
#recruitment$log_sigma_recruit[1]$value <- log(parfinal$sigmaR)
recruitment$log_rzero[1]$value <- parfinal$mean_log_recruit + log(1e9)
recruitment$log_rzero[1]$estimation_type$set("fixed_effects")
## note: do not set steepness exactly equal to 1, use 0.99 instead in ASAP run
recruitment$logit_steep[1]$value <-
-log(1.0 - .99999) + log(.99999 - 0.2)
recruitment$logit_steep[1]$estimation_type$set("constant")
recruitment$nyears$set(n_years - 1)
recruitment$log_devs$resize(n_years - 1)
for (y in seq(n_years - 1)) {
recruitment$log_devs[y]$value <- parfinal$dev_log_recruit[y+1]
}
recruitment$log_devs$set_all_estimable(estimate_recdevs)
recruitment$log_devs$set_all_random(TRUE)
recruitment_distribution <- methods::new(DnormDistribution)
# set up logR_sd using the normal log_sd parameter
# logR_sd is NOT logged. It needs to enter the model logged b/c the exp() is
# taken before the likelihood calculation
recruitment_distribution$log_sd <- methods::new(ParameterVector, 1)
recruitment_distribution$log_sd[1]$value <- log(parfinal$sigmaR)
recruitment_distribution$log_sd[1]$estimation_type$set("constant")
recruitment_distribution$x$resize(n_years - 1)
recruitment_distribution$expected_values$resize(n_years - 1)
for (i in seq(n_years - 1)) {
recruitment_distribution$x[i]$value <- 0
recruitment_distribution$expected_values[i]$value <- 0
}
recruitment_distribution$set_distribution_links("random_effects", recruitment$log_devs$get_id())
## growth -- assumes single WAA vector for everything, based on
## Srv1 above
waa <- pkinput$dat$wt_srv1
waa <- rbind(waa, waa[1, ])
ewaa_growth <- methods::new(EWAAGrowth)
ewaa_growth$n_years$set(get_n_years(data_4_model) + 1)
ewaa_growth$ages$resize(n_ages)
purrr::walk(
seq_along(ages),
\(x) ewaa_growth$ages$set(x - 1, ages[x])
)
ewaa_growth$weights$resize(n_ages * (get_n_years(data_4_model) + 1))
purrr::walk(
seq(ewaa_growth$weights$size()),
\(x) ewaa_growth$weights$set(x - 1, c(t(waa))[x])
)
## NOTE: FIMS assumes SSB calculated at the start of the year, so
## need to adjust ASAP to do so as well for now, need to make
## timing of SSB calculation part of FIMS later
## maturity
## NOTE: for now tricking FIMS into thinking age 0 is age 1, so need to adjust A50 for maturity because FIMS calculations use ages 0-5+ instead of 1-6
maturity <- methods::new(LogisticMaturity)
maturity$inflection_point[1]$value <- 4.5
maturity$inflection_point[1]$estimation_type$set("constant")
maturity$slope[1]$value <- 1.5
maturity$slope[1]$estimation_type$set("constant")
# population
population <- methods::new(Population)
tmpM <- log(as.numeric(t(matrix(
rep(pkfitfinal$rep$M, each = n_years), nrow = n_years
))))
population$log_M$resize(n_years * n_ages)
for (i in seq(n_years * n_ages)) {
population$log_M[i]$value <- tmpM[i]
}
population$log_M$set_all_estimable(FALSE)
population$log_init_naa$resize(n_ages)
initNAA <- c(log(pkfitfinal$rep$recruit[1]), log(pkfitfinal$rep$initN)) + log(1e9)
for (i in seq(n_ages)) {
population$log_init_naa[i]$value <- initNAA[i]
}
population$log_init_naa$set_all_estimable(FALSE)# NOTE: fixing at ASAP estimates to test SSB calculations
population$nages$set(n_ages)
population$ages$resize(n_ages)
purrr::walk(
seq_along(ages),
\(x) population$ages$set(x - 1, ages[x])
)
population$nfleets$set(4)
population$nyears$set(n_years)
population$nseasons$set(1)
population$SetMaturityID(maturity$get_id())
population$SetGrowthID(ewaa_growth$get_id())
population$SetRecruitmentID(recruitment$get_id())
# Change the year range back to true
years <- 1970:2023
# build object but DO NOT optimize it, pass the original MLE to it
obj_nodata <- TMB::MakeADFun(
data = list(),
parameters,
DLL = "FIMS",
silent = TRUE,
random = "re"
)
success <- FIMS::CreateTMBModel()
parameters <- list(p = get_fixed())
parameter_names <- names(FIMS:::get_parameter_names(obj[["par"]]))
# vector of which are affected by priors/penalties
lrandom <- is.na(parameter_names)
# the cAIC calculations
hess_data <- obj$he(mle)[lrandom, lrandom]
hess_no_data <- obj_nodata$he(mle)[lrandom, lrandom]
neg_edf <- diag(solve(hess_data, hess_no_data))
# some data processing
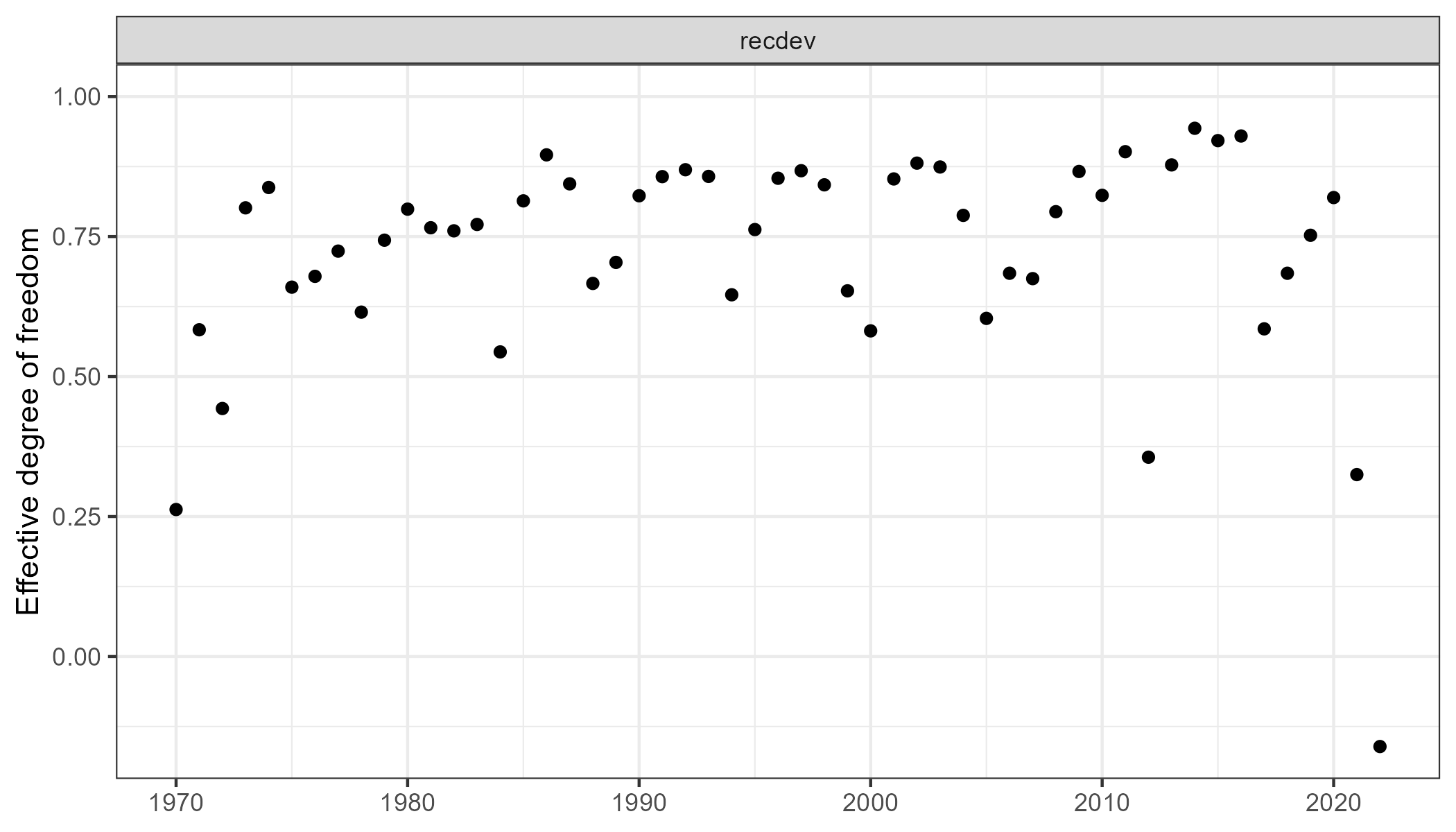
edf <- data.frame(par = "recdev", n = 1, edf = 1 - neg_edf) |>
dplyr::mutate(year = 1969 + 1:n()) |>
dplyr::ungroup()
g <- ggplot2::ggplot(edf, ggplot2::aes(year, y = edf)) +
ggplot2::geom_point() +
ggplot2::facet_wrap("par") +
ggplot2::labs(x = NULL, y = "Effective degree of freedom") +
ggplot2::ylim(NA, 1)
ggplot2::ggsave("figures/cAIC_edf.png", g, width = 7, height = 4)
tab <- edf |>
dplyr::group_by(par) |>
dplyr::summarize(n = sum(n), edf = sum(edf)) |>
dplyr::arrange(desc(edf))
tab <- dplyr::bind_rows(
tab,
edf |>
dplyr::summarize(par = "Total", n = sum(n), edf = sum(edf))
) |>
dplyr::mutate(pct = 100 * edf / n)
gt::gt(tab) |> gt::fmt_number(columns = 3:4, decimals = 1)
q <- sum(lrandom) # no. of random effects
p <- sum(1 - lrandom) # no. of fixed effects
jnll <- obj$env$f(mle)
cnll <- jnll - obj_nodata$env$f(mle)
## conditional AIC (new calculation)
cAIC <- 2 * cnll + 2 * (p + q) - 2 * sum(neg_edf)
round(
c(
edf = sum(edf$edf),
pct.edf = 100 * (sum(edf$edf) / sum(edf$n)),
cAIC = cAIC,
mAIC = TMBhelper::TMBAIC(opt)
),
1
)